1. 直交射影 (Orthogonal Projection)

直交射影は、点をその垂直方向に平面や直線に投影する方法です。例えば、3次元空間の点を2次元平面に直交的に射影する場合、その点と平面の間に垂直な線を引き、その線が平面と交わる点が射影点となります。

特徴:

• 垂直な方向に射影する。
• 点と平面または直線の間の最短距離が計算される。

2. 斜投影 (Oblique Projection)

斜投影は、直交射影とは異なり、任意の角度で射影を行う方法です。これにより、射影面に対して斜めにオブジェクトが投影されます。

特徴:

• 任意の角度で射影する。
• 立体的な効果を維持しながら2次元に投影できる。

3. 透視投影 (Perspective Projection)

透視投影は、カメラのレンズや人間の目による視覚と同様の方法で、3次元オブジェクトを2次元平面に投影する方法です。遠くの物体は小さく、近くの物体は大きく見えるという特性を持っています。

特徴:

• 視点（カメラまたは観察者の位置）からオブジェクトを投影。
• 遠近法を用いて現実に近い描写が可能。

4. 平行投影 (Parallel Projection)

平行投影は、投影線がすべて平行である方法です。平行投影には、等角投影（isometric projection）や斜投影（oblique projection）が含まれます。

特徴:

• 投影線が平行であるため、遠近感がない。
• 工学図面やCADで使用される。

数学的な表現

プロジェクションの数学的な表現は行列を用いて行われることが多いです。

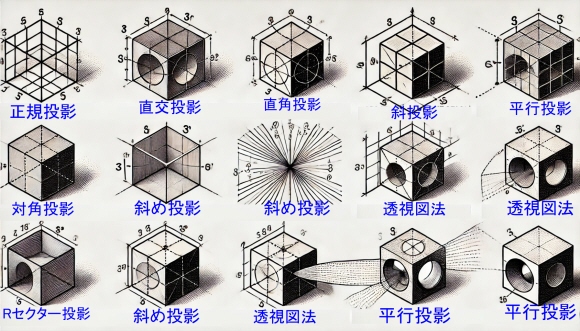数学や幾何学におけるプロジェクションのイメージ画像です。直交射影、斜投影、透視投影、平行投影のそれぞれの種類と、それらの3Dオブジェクト（例えば、キューブ）の2D平面への投影を示しています。各プロジェクションの種類が明確にラベル付けされています。