有限要素解析（FEM: Finite Element Method）は、物理現象のシミュレーションや構造解析に広く用いられる数値解析手法です。FEMは、複雑な形状や材料特性を持つ構造物や部品を小さな要素に分割し、それぞれの要素ごとに方程式を解くことで、全体の応答を計算します。

有限要素解析の主な手順

1.モデル化: 解析対象の構造物や材料を仮想的にモデル化し、有限要素に分割します。このとき、形状や材料の特性に応じてメッシュを生成します。メッシュの密度（細かさ）は解析精度に大きく影響します。

2.境界条件と荷重の設定: 解析対象にかかる力や温度、固定された部分などの境界条件を設定します。

3.方程式の解法: 各要素ごとの方程式を連立して解き、対象全体の変形や応力、温度分布などを計算します。これには線形代数や非線形方程式の数値解法が用いられます。

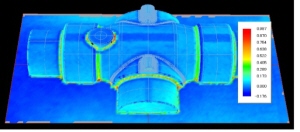
4.結果の可視化: 解析結果を視覚的に表示し、変形量や応力分布、温度分布などを評価します。これにより、設計の改善点を発見したり、問題の予測が可能になります。

利用分野

・機械工学: 自動車、航空機、家電製品などの部品強度や応力解析

・土木工学: 建物や橋梁の耐久性、地震時の変形解析

・医療工学: 人体の骨や人工関節の応力分布のシミュレーション

・電気工学: 電磁場解析や熱伝導解析

FEMは、手計算や実験では難しい複雑な問題も、精密にシミュレーションするのに有効な手法として発展しています。